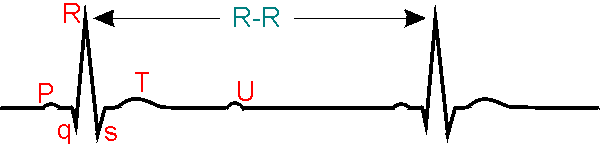
1. Дипломната работа е публикувана в оригинал. По времето когато е писана (1992г.) още не беше излязла статията за стандартизиране на параметрите при измерване на вариативността на сърдечния ритъм (Heart Rate Variability)*.
2. Повечето от графиките липсват, поради факта, че архива беше на флопидискове с обем 360к (!) а те не бяха най-надеждния носител :( Ако все пак се интересувате от някоя конкретна графика, пишете ми и аз ще се опитам да я възстановя (както съм направил с останалите графики - генерирал съм ги отново).
3. Ако някои от нещата ви се струват наивни, (например допотопните падащи менюта в текстов режим на DOS) спомнете си (ако сте били родени вече) какъв беше софтуера в далечната 1992 година ;)
(*) Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Heart rate variability: standards of measurement, physiological interpretation and clinical use. Circulation. 1996 Mar 1;
-----------------------------
Очаквам всякакви коментари на адрес: mlab-AT-mail-DOT-bg
С Ъ Д Ъ Р Ж А Н И Е
В медицината широко се използва електрокардиографския метод за изследване на сърдечната дейност. Той регистрира преразпределението на биотоковете в сърдечния мускул, в следствие на деполяризация и реполяризация на неговите клетки (от възбудно-проводната тъкан на миокарда) [32].
В електрокардиограмата (ЕКГ) има няколко характерни области, които е прието да се бележат с латинските букви P, Q, R, S, T (понякога се наблюдава и допълнителна шеста област - U):
фиг.1
По тяхната форма, амплитуда и продължителност могат да се диагностицират различни морфологични и функционални заболявания на миокарда. За съжаление обаче, този метод има едно съществено ограничение - той не може да ни даде информация за динамиката на регулаторните процеси в сърдечно-съдовата система (а от тук и за функционалното състояние на организма). Представа за тези процеси може да се получи като се изследва вълновата структура на сърдечния ритъм, чрез продължителен запис (обикновено 3 - 20 мин.) на R-R интервали [10,11,15] (под R-R интервал се разбира разстоянието между два съседни R-зъбци в ЕКГ; виж фиг.1).
Въпреки, че началото на сърдечния цикъл започва от момента на възбуждането на клетките от синусовия възел (на ЕКГ това е P-вълната, която се получава при деполяризация на предсърдията), за изследване на сърдечния ритъм се прави запис на R-R интервалите, тъй-като R-зъбците се отчитат по-лесно и по-точно отколкото P-вълните. Това се дължи на факта, че амплитудата на R-зъбеца е многократно по-голяма от амплитудата на P-вълнaта, независимо от отвеждането (начина, по който са разположени електродите по тялото). При това грешката от използването на R-зъбците вместо P-вълните е от порядъка на 2 до 5 мсек.(с толкова може да варира разстоянието между P-вълната и QRS-комплекса в зависимост от флуктоациите в проводимостта на атриовентрикуларния възел [3]), което е пренебрежимо малко в сравнение с продължителността на интервалите (примерно 1сек. при 60 уд./мин) [7].
Оценката на функционалното състояние на организма по характера на регулацията в сърдечно-съдовата система се основава на представянето на вълновата структура на сърдечния ритъм като суперпозиция от колебателните процеси на основните функционални системи (централна нервна система, вегетативна нервна система и т.н.) [13,15].
Особено внимание се обръща на влиянието на симпатиковата и парасимпатиковата подсистеми на вегетативната нервна система върху сърдечния ритъм. В това отношение са направени редица модели [3,4,7,11,31], имащи за цел обстойното изучаване на това влияние. Най-често използвания от тях е IPFM (Integral Pulse Frequency Model), предложен за първи път от Hyndman [33]. По същество този модел представя синусовия възел като генератор, чиято честота се модулира от симпатикуса и парасимпатикуса. Значителен принос в доразработването и доказването на състоятелността на този модел, имат опитите, проведени с животни, при които тези две подсистеми се възбуждат независимо една от друга, като по този начин се наблюдава влиянието на всяка една от тях върху сърдечния ритъм [30].
Върху дължината на R-R интервалите влияние оказват не само вътрешни (както вече бе споменато това са основните функционални системи),но и външни по отношение на организма фактори (температура, налягане и т.н.), които в общия случай имат недетерминиран характер. Това ни дава основание при математическия анализ на сърдечния ритъм, да разглеждаме реда от R-R интервали като случаен процес. При това, става дума за нестационарен случаен процес. И наистина, ако се разглежда запис, чиято продължителност се измерва в минути, в сърдечния ритъм се наблюдават процеси, които не могат да се интерпретират като стационарни. Такива са например апериодичните колебания, свързани с дълбоки вдишвания.
Наред с нестационарните, в сърдечния ритъм се наблюдават и относително устойчиви колебателни съставящи. Те могат да бъдат свързани със саморегулацията на сърдечно-съдовата система, циклически процеси в организма (например дишането) и други негови функции.
Често използвани методи за изследване на вълновата структура на сърдечния ритъм са корелационният [9,11] и най-вече спектралният [1,4,7,8,10,12] анализ. Обикновено, интерес при тези анализи представляват няколко честотни диапазона [2,4,8,12], които се срещат под различни наименования:
Съществуват различни (спорни) мнения за произхода на отделните вълни (особено за БВ1 и БВ2), но факта, който никой не оспорва е, че тези вълни съдържат информация за функционалното състояние на организма.
В дипломната работа са разгледани някои от методите за анализ на R-R интервали, като основно внимание се обръща на спектралния анализ. Дадено е и описание на създадената от нас система за анализ на сърдечния ритъм - CardioLab.
Авторът изказва сърдечна благодарност на гл.ас. к.м.н. Емилия Павлова, д-р Любомир Петров и д-р Любен Грънчаров, за плодотворното сътрудничество при създаване на системата CardioLab, както и за любезно предоставените от тяхна страна литература и резултати от проведени изследвания, за съставянето на настоящия труд.
В тази глава ще направя кратък обзор на методите за цифрова обработка на сигнали, чието все по-широкото навлизане в практиката е обусловено от нарастващата (бих казал по експоненциален закон) изчислителна мощ на компютърните системи през последното десетилетие.
За да може един непрекъснат във времето сигнал да се обработи с цифров метод е необходимо първо той да бъде дискретизиран. Това означава той да стане функция на дискретното време kTo.
(1.1) x(t) -> дискр.(To) -> y(kTo) , k = 0,1,2,...
където To е такта на дискретизация, k е номера на отчета (вместо kTo може да се използва само k).Теоремата на Котелников-Шенон [19,21] дава необходимото условие за възстановяване на непрекъснатия сигнал:
(1.2) Tomax = 1/(2Fmax) ,
където Tomax е най-големия период на дискретизация, а Fmax е максималната честота, съдържаща се в изходния сигнал. Както се вижда от формулата, ограничението за To е само в едната посока (от горе) т.е. ние можем да изберем такт, който е по-малък от Tomax. И на практика точно така се прави с цел по-голяма точност на извършваните обработки. Но има ограничения и за долната граница на To , макар и не толкова твърди. Те се дължат на крайната дължина на машинната дума и ограничения във времето, необходимо за обработките [21].
Това е всъщност обратната операция на дискретизация. Съществуват много методи за интерполация - линейна, квадратична, кубична, чрез интерполационни полиноми (Нютон, Лагранж [27] и др.), сплайн интерполация и т.н. В зависимост от решаваните проблеми се избират различни по сложност методи.
Това е една от най-често срещаните обработки не само във временната, но и в честотната област. Това се дължи на факта, че чрез нея се решават много, и разнообразни по своя характер задачи.
Често използвани са така наречените рекурсивни (1.3) и нерекурсивни (1.4) линейни филтри:
(1.3) ![]()
(1.4) ![]()
където u(k) е входния сигнал, y(k) - филтрирания сигнал, a a(k) и b(k) са коефициентите на филтъра.
При рекурсивните филтри изходния сигнал y(k) зависи от m+1 стойности на входния сигнал и от n предходни стойности на изходната поредица. При нерекурсивните филтри y(k) в момента от време k зависи само от стойността на входната поредица в този момент и от m предходни стойности на входния сигнал.
Когато сигнала, който искаме да обработваме е силно зашумен удачно е да се използва оптималния (по отношение на минимума на ковариационната матрица на грешката) филтър на Калман [20].
В много случаи филтрация, близка до оптималната може да се постигне и с цифрови филтри от по-нисък ред. Например експоненциален филтър, чието диференчно уравнение изглежда по следния начин:
(1.5) y(k) = (1-с)*y(k-1) + с*u(k)
За да има изглаждащи свойства, параметъра “с” трябва да приема стойности между 0 и 1. Установено е, че оптимална филтрация се получава при стойности на с в интервала (0.4 - 0.7). Широкото приложение на този филтър се дължи на неговата слаба чуствителност към неточно задаване на статистическите свойства на сигнала и шума [20].
Всички обработки в честотната област, неизбежно са свързани с понятието спектър. Ето защо е необходимо да се даде определение на това понятие, но преди това нека въведем следното представяне на произволен дискретен сигнал s(n), зададен за интервал от N точки:
Тук {![]() }
е съвкупност от базисни функции, определени за
същия интервал; {X(k)} - коефициенти на разложението
на сигнала по базисните функции ; Ek - енергия на
k-тата базисна функция. Сега вече може да се даде
следното определение: Спектър се наричат
коефициентите (X(k)), получени при разложението на
сигнала в базис от ортогонални функции (
}
е съвкупност от базисни функции, определени за
същия интервал; {X(k)} - коефициенти на разложението
на сигнала по базисните функции ; Ek - енергия на
k-тата базисна функция. Сега вече може да се даде
следното определение: Спектър се наричат
коефициентите (X(k)), получени при разложението на
сигнала в базис от ортогонални функции (![]() ) [16].
) [16].
Във формула (1.6) имаме безкрайна сума. Това прави невъзможно практическото използване на това представяне. Ето защо по-голям интерес за задачите на цифровата обработка на сигнали представляват случаите когато броят на базисните функции е равен на размерността на сигнала (N).
Възниква резонния въпрос - какви базисни функции да изберем? Обикновено избора зависи от специфичните особености на решаваната задача и от съображения за математически удобства.
Например ако сигнала, чийто спектър искаме да намерим, е съставен от правоъгълни функции удачно е да използваме за базис функциите на Уолш (трансформацията, базираща се на функциите на Уолш е известна като преобразувание на Адамар [16]). Ако пък имаме сигнал, получен например от наслагване на хармонични съставки, то най-добре е в случая да използваме базиса на основната тригонометрична система функции (1.8) (например преобразувание на Фурие):
(1.8) 1,cos(x),sin(x),cos(2x),sin(2x),...
Освен споменатите по-горе съображения, при избора на базисни функции, трябва да се спазят и определени математически изисквания [27]. Това прави избора на базис не толкова тривиална задача, колкото изглежда на пръв поглед. Но в техническата литература има достатъчно трансформации (Фурие, Хартли, Уолш-Адамар, Хаар, Хотелинг ...), които биха задоволили и най-капризните изисквания към спектралния анализ, така че няма нужда да избираме базис, а направо избираме подходяща за случая трансформация.
От двете формули (1.6) и (1.7) може да се направи извода, че връзката сигнал - спектър е еднозначно определена. На всеки сигнал съответства спектър и на всеки спектър съответства сигнал. Това е едно от важните свойства на спектралното преобразувание, което до голяма степен обуславя неговото широко приложение.
Спектралната трансформация е един изключително мощен, но в същото време и доста капризен метод за обработка на сигнали. И ако не се погрижим да премахнем предварително някои нежелани ефекти, резултатите ще бъдат незадоволителни, а в някои случаи дори подвеждащи.
Нека имаме сигнал със силно изразен линеен тренд. При спектралната трансформация, линейния тренд ще доведе до появяване на мощен пик в ниските честоти. И тъй-като данните трябва да се скалират, за да могат да се покажат в графичен вид, този пик ще подтисне останалите честоти и ние няма да получим реална представа за хармоничните съставящи на сигнала.
Същото се отнася и за сезонния тренд, само че пикът ще се появи на честота, съответстваща на сезонния период.
Ето защо преди спектралното преобразувание, сигналът трябва да се изчисти от тренда. Това може да стане чрез линейна регресия (за линейния тренд) ,или чрез диференчни филтри (за сезонен тренд):
(1.9) y(t) = x(t) - x(t-s) ,
където s е броят на сезоните. В частност при s=1, се премахва линеен тренд [22].
Спектралната трансформация предполага периодичност на входния сигнал, което води до появата на 'лъжливи' пикове в спектъра, дължащи се на периодичното продължение на временната функция. Това явление е известно като изтичане на мощност. За да се намали ефекта от него се използват така наречените корелационни прозорци, които плавно доближават краищата на сигнала до нулата. Някои от по-често използваните корелационни прозорци са следните: правоъгълен, триъгълен (Бартлет), Хан, Хеминг, Блекмън [18].
Тази операция също може да намали ефекта от изтичането на мощност, но освен това служи и за сгъстяване на честотната скала. Тя се извършва просто като допълним реда с необходимия брой нули.
Изглаждането може да се извърши както във временната, така и в честотната област. Ефектът е един и същ - премахват се от спектъра несъществените пикове и той става по-ясен. Извършва се обикновено по метода пълзящо средно (всяка стойност на реда се замества със средната от няколко стойности):
(1.10) ![]() ; i=1,2,..,(n-k+1)
; i=1,2,..,(n-k+1)
Трябва внимателно да се подбере дълбочината на изглаждане (k), в противен случай може да се загуби полезна информация.
Най-често спектралните преобразувания се използват за намиране на спектралната плътност (мощност) S(f) на сигнала:
(1.11) ![]()
където X(f) е спектъра на сигнала, получен в резултат на спектрална трансформация.
Ако спектъра е получен например чрез ПФ (преобраз. на Фурие), той ще е комплексна функция на кръговата честота w (X(jw)), но неговата спектрална плътност ще бъде отново реална функция:
(1.12) ![]()
тук с ![]() е означена комплексно-спрегнатата
функция на X(jw).
е означена комплексно-спрегнатата
функция на X(jw).
Физическия смисъл на спектралната плътност е, че тя отразява мощността на сигнала по честоти.
В края на точка 2.1. беше направен важен извод, според който можем еднозначно да преминаваме от временната в честотната област и обратно. Тогава е възможна следната процедура - преминаване в честотната област, обработване на спектъра и връщане отново във временната област. При това обработките върху спектъра ще доведат до съответстващи изменения и върху изходния сигнал във временната област.
Ако от спектъра на сигнала сме премахнали пик, съответстващ на честота fc , то при обратното преобразуване на сигнала ще се окаже, че съставката с честота fc е филтрирана т.е. все едно, че сигнала е преминал през режекторен филтър с честота на подтискане fc.
Много често в практиката се налага извършване на операцията свиване на два сигнала.
(1.13) ![]() ; n = 0,1,..,L+M-2
; n = 0,1,..,L+M-2
където {h(k)} и {s(k)} са входните последователности с дължини съответно L и M , а y(n) е изходната последователност с дължина L+M-1.
Съществува следното свойство на спектралното преобразувание: Ако {y(k)} е редица, получена в резултат на свиване на редиците {h(k)} и {s(k)} то:
(1.14) Y(f) = H(f)S(f) ,
където Y(f), H(f) и S(f) са съответно образите на сигналите y(k), h(k) и s(k) в честотната област. Или с други думи на операцията свиване във временната област съответства операция умножение в честотната област. Това свойство се използва за бързо изчисляване на свиването (съществуват и други бързи методи за изчисляване на свиването, между които са теоретико-числовите преобразувания и китайската теорема за остатъците [16]).
Корелационната функция е важна характеристика на сигнала, която дава зависимостта между извадки от редицата в различни моменти от време:
(1.15) ![]() ;
; ![]()
По вида на ![]() можем например да разберем
дали реда, който изследваме е стационарен (при
стационарен ред
можем например да разберем
дали реда, който изследваме е стационарен (при
стационарен ред ![]() е затихваща [28]), можем също така да
определим периода на хармоничните съставки и т.н.
е затихваща [28]), можем също така да
определим периода на хармоничните съставки и т.н.
Но пресмятането на ![]() по формула (1.15)
би ни отнело прекалено много време за да си
позволим лукса да я използваме. На помощ отново
идва спектралното преобразувание и по-скоро
изчислената чрез него спектрална плътност S(f). В
сила е следната обратима връзка:
по формула (1.15)
би ни отнело прекалено много време за да си
позволим лукса да я използваме. На помощ отново
идва спектралното преобразувание и по-скоро
изчислената чрез него спектрална плътност S(f). В
сила е следната обратима връзка:
(1.16) ![]() ---> спектрална трансф.---> S(f)
---> спектрална трансф.---> S(f)
(1.17) S(f) ---> обратна сп.трансф.---> ![]()
Кроскорелационната функция (или взаимна корелационна функция), подобно на корелационната (или още автокорелационна) дава степента на връзката (корелацията) между два сигнала:
(1.18) ![]() ; i = 1,2,..,N
; i = 1,2,..,N
Формулите (1.16) и (1.17) са в сила и за ![]() , като S(f) се
замени с Sxy(f) (която за разлика от S(f) няма
конкретен физически смисъл).
, като S(f) се
замени с Sxy(f) (която за разлика от S(f) няма
конкретен физически смисъл).
За да бъде коректен спектралният анализ е необходимо данните, които се изследват да бъдат функция на времето (за да може спектърът да е ф-я на честотата). В противен случай спектърът няма да може да се интерпретира правилно.
Реда от R-R интервали, който ние получаваме е функция на номерата на интервалите. Следователно той трябва така да се преработи (регуляризира), че да стане функция на времето.В литературата има описани различни методи за регуляризация [1,7,12].
В системата CardioLab се използва следния метод: прави се линейна интерполация на кардиоинтервалите за да се получи непрекъсната функция на времето и след това получената функция се дискретизира (Td). Не случайно е избрана линейна а не някакъв друг вид интерполация. Този избор е свързан с инертността на сърдечната дейност - съществуват така наречените компесаторни паузи, през които клетките на миокарда не могат да бъдат възбудени.
Едно от предимствата на този метод пред останалите е, че с промяната на Td можем да избираме произволен (разбира се има известни ограничения, произтичащи от дължината на реда) честотен диапазон на спектралната трансформация.
В системата CardioLab спектралния анализ се извършва чрез БПХ (бързо преобразувание на Хартли [17]). Този избор бе направен след като бяха извършени редица експерименти с три спектрални трансформации - БПФ (бързо преобразувание на Фурие), БПА (бързо преобразувание на Адамар) и БПХ.
Резултатите от теста за скорост показаха, че най-бързо е БПА, след него БПХ и накрая БПФ. Това е лесно обяснимо - при БПА имаме само операции събиране и изваждане, които отнемат малко машинно време, за разлика от умножението, което се използва при БПФ и БПХ. Комплексните числа, използвани при БПФ (а от тук и необходимостта да се обработват два масива - за реалните и за имагинерните части), му отреждат последното място в класацията за скорост.
При теста за точност последното място зае БПА. Този резултат също не е изненадващ. При този тест входния сигнал се образува като сбор от две синусоиди и адитивен шум с равномерно разпределение (предполага се, че изследваните данни имат подобен състав). И тъй-като БПА се опитва да разложи сигнала в базис на Уолш [16], който е съставен от правоъгълни функции, получава се изтичане на мощност, което прави БПА неприложимо за изследване на хармонични сигнали (по принцип БПА се използва за кодиране на информация и при обработка на изображения).
Симетричността на правото и обратното БПХ (и двете се извършват с една и съща формула) окончателно реши въпроса за избор на спектрална трансформация.
Спектралният анализ се използва за определяне честотата на дихателните вълни, бавните вълни от 1-ви и 2-ри порядък, както и произволни други хармонични съставки на сърдечния ритъм [1,7,8,10,12]. Освен това могат да се намерят и съотношенията на техните мощности.
За да се получат информативни и най-вече верни резултати е необходима много добра предварителна подготовка на данните. Още при избора на област, (на която ще правим спектрален анализ) тя трябва да е сравнително стационарна. Ако има артефакти и/или екстрасистоли те трябва да се изчистят. Премахването на линейния тренд (особено ако е силен) ще подобри до голяма степен резултатите.
Изобщо всички предварителни обработки, разгледани в Глава 1 (точка 2.2.) трябва да се имат предвид. Необходимо е към всеки запис да се подходи строго индивидуално, в зависимост от параметрите, които искаме да оценим и от вида на самите данни.
Например ако ни интересува само честотата на бавните вълни от 2-ри порядък можем спокойно да филтрираме по-бързите вълни [10] или пък да увеличим такта на дискретизация и по този начин да наблюдаваме с подробности само ниско-честотния диапазон.
Спектралният анализ на сърдечния ритъм намира широко приложение в кардиологията, спортната медицина (отчита физиологични параметри при различни натоварвания), фармакологията (тестване на лекарствени препарати), психологията и т.н. Изобщо той може да бъде използван навсякъде където е необходимо да се следи динамиката във регулаторните функции на организма - например при практикуващи трансцедентална медитация (виж Глава 4).
В системата CardioLab е предвиден специален режим (Spectral analysis) за спектрален анализ (фиг.2.1). В него са включени някои от предварителните обработки, които се избират чрез опции (обработките, които не са включени в този режим, могат да се извършат предварително в някой от другите режими).
фиг.2.1
На фиг.2.1 е показана спектралната плътност на избрана област от данните (бялата лента под R-R интервалите). Ясно личат пиковете, съответстващи на бавните вълни от 2-ри и 1-ви порядък и на дихателните вълни. Показано е отношението между мощностите (интегралите) на двата избрани честотни диапазона (белите полета под спектрограмата) и мощността на всеки един от тях в проценти.
Хистограма на R-R интервалите се строи като абсцисата се раздели на диапазони, в които могат да попадат данните, а по ординатата се нанесат броя на попаденията в съответния диапазон. Дават се различни препоръки за минималния брой диапазони в зависимост от броя на данните [29], който гарантира информативност на представянето. По-големия брой диапазони означава по подробна хистограма.
В нашата система броя на диапазоните е фиксиран, като е избрано число (k=40), което надхвърля всички изисквания дори при максимално-допустимия брой на данните (MAXARR=2048).
При представянето на данните във вид на хистограма могат да се определят следните параметри: мода (Mo), амплитуда на модата (Am) и широчината на диапазоните (dx). Интерес представлява и самия вид на хистограмата, по който може да се съди за типа на разпределението на данните.
Обикновено хистограмата се използва съвместно с други методи за обработване на данните [2,4,11,23]. Самата тя не може да ни даде пълна и най-вече еднозначна представа за характера на данните, т.к. два различни процеса могат да имат сходни (дори еднакви) хистограми.
При анализа на сърдечния ритъм често се строят хистограми и за други данни, не само за R-R интервали [5].
Системата CardioLab построява хистограма на данните, като използва едновременно два начина на разделяне на абсцисата - абсолютно (хоризонталната ос е разграфена от 0 до 2000 мсек.) и относително (от минималния до максималния кардиоинтервал). Относителното скалиране дава максимално-възможната информация за текущите данни, а абсолютното позволява сравняване на различни данни.
На фиг.2.2 е показана хистограма, скалирана по двата начина (горната-относително, долната-абсолютно).
фиг.2.2
Скатерограмата е един вид корелационно поле, тъй-като отразява връзката между съседни R-R интервали. Тя се построява като множество от точки с координати (Ri,Ri+1), където Ri е i-тия R-R интервал. По този начин всеки R-R интервал (с изключение на първия и последния) участва последователно и като абсциса, и като ордината.
На фиг.2.3 е показана скатерограма, скалирана по двата начина (относително и абсолютно).
фиг.2.3
Ако в данните има силно-различаващи се R-R интервали (например артефакти), ще се появят две области, отдалечени от нормално-разположените R-R интервали. При наличие на екстрасистоли, отново ще се получат характерни области ,различни от тези при артефактите. Това дава възможност скатерограмата да се използва при откриването на артефакти и екстрасистоли [24].
Когато броят на изследваните R-R интервали е голям, скатерограмата не може да ни даде представа за 'мощността' (броя на попаденията) в отделните области. Ето защо в системата CardioLab е предвидена възможност за построяване на обемна скатерограма, която ни дава допълнителна информация за отделните области от двумерната скатерограма.
фиг.2.4
Дадена е височина (в брой R-R интервали) на най-високия стълб, както и широчината на интервалите (dx).
Стандартен начин за представяне на ритмограмата (наричана още тахограма или пулсограма) е когато по абсцисата се нанесат номерата, а по ординатата дължините на R-R интервалите. Използват се и други форми на представяне, при които по ординатата не се нанася дължината на кардиоинтервала а някаква друга (зависеща от него) характеристика. Например пулсова честота (обикновено дименсията е удари/мин.).
Ритмограмата е най-често използвания метод за графично представяне на R-R интервалите, т.к. показва 'суровия' вид на реда. От нея може да се получи начална представа за вълновата структура на процеса и за наличието на артефакти или екстрасистоли. Именно чрез ритмограмата се избират стационарни участъци [11], на които се прави спектрален анализ.
Освен като съпътстващ метод за представяне, ритмограмата се използва и за анализ на преходните процеси в регулацията на сърдечната дейност [10,13,14,15].
На фиг.2.5 е дадена ритмограма, отново скалирана по двата метода.
фиг.2.5
При статистическата обработка на R-R интервалите освен стандартните статистики (средна стойност, средно-квадратично отклонение, дисперсия и т.н.) се използват и специфични статистически показатели (виж [26] и Глава 3 точка 2.3.2.), които в последствие могат да се използват като изходни данни за дискриминантен и клъстерен анализ.
Изискванията към конфигурацията, на която ще работи системата, са минимални: PC XT/AT, 256K RAM, 1 паралелен порт и флопи 360К. Ограничения по отношение на монитора и видеокартата няма. При липса на паралелен порт, програмата може само да обработва предварително снети данни, но не и да прави запис от външен източник.
Данните могат да се четат от стандартен ЕКГ-монитор (всички по-нови модели имат вграден R-R идентификатор) или от специално разработен за целта R-R детектор. И в двата случая четенето става през принтерския порт (краче 12 - Paper End). При всеки постъпил импулс първо се прочита стойността от брояча на времето, след което се нулира. И тъй-като канал 0 на таймера е инициализиран да дава прекъсване на 1мсек.(само за времето на експеримента), интервала между два постъпили импулса се измерва с точност около 1мсек., която е напълно достатъчна за случая.
Преди да се нулира брояча на времето, неговата стойност се запазва и след приключване на записа се използва (след като се сумира с изтеклото време) за възстановяване на системния часовник.
Програмният пакет CardioLab се състои от 8 модула, написани на Turbo C, които се компилират самостоятелно и след това се свързват в един общ изпълним файл. За по-голямо удобство декларирането на глобалните функции и променливи, както и дефинирането на макросите е направено в отделни хедър-файлове.
Диалога с потребителя е организиран на принципа на "падащите прозорци". Основните подменюта са 8 на брой и избора на всяко едно от тях става чрез стрелките или чрез осветените букви (първите букви от наименованията на менютата).
Следва кратко описание на различните подменюта по реда, в който те са разположени в главното меню.
Благодарение на някои от тях, системата има възможност както да обработва данни, получени от произволни други програми, така и да създава текстови файлове, които могат да се прочетат и обработят от който и да е текстови редактор или електронна таблица. Това разширява до голяма степен възможностите на системата.
2.1.1 Load File - зарежда в паметта на компютъра файл с данни, имащи следния формат:
CardioLab <Sw> <Nr> <Id> <FrText> #
<Data> EOF
CardioLab - задължителна ключова дума в началото на
файла
<Sw> - T-текстов, B-двоичен вид на Data
<Nr> - брой на данните във файла
<Id> - идентификатор за вида на данните (пр. R-R)
<FrText> - свободен текст
# - маркер за начало на валидните данни
<Data> - данни (вида им зависи от Sw)
EOF - стандартен маркер за край на файла
2.1.2. Save File - записва на диск данните от паметта на компютъра. Полученият файл има гореописания формат като Sw='B' т.е. данните са записани в двоичен вид (за всяко число се отделят два байта).
2.1.3. Delete File - изтрива файл (преди това иска потвърждение).
2.1.4. View File - показва на екрана произволен текстов файл. Дава възможност за временно спиране на листинга с цел разглеждане съдържанието на файла.
2.1.5. Change Dir - сменя текущата директория.
2.1.6. Save TextFile - записва данните от паметта на компютъра в текстов вид т.е. Sw='T'. По този начин данните могат да се разгледат чрез 'View File'.
2.1.7. Exit to DOS - изход в DOS (иска потвърждение).
Всички функции от това подменю (с изкл. на последната) ползват подпрограма за четене на стринг от клавиатурата, която поддържа всички редактиращи клавиши и следи за дължината на въвежданите стрингове.
Тъй-като отделните функции имат самостоятелни статични буфери, при всяко извикване на някоя от тях по подразбиране се появява последния въведен стринг. Това е особено полезно при 'Load File' когато анализираме данни от няколко експеримента и можем да въведем подходяща маска, която да ни листва само файловете от един (или няколко) експеримента. Например - Load File Name: a:\exp1*.ecg
Помощни функции за обработка на данните в паметта на компютъра.
2.2.1 Customize - тази функция дава възможност на потребителя да извършва следните операции над данните:
На фиг.3.1 е показан графичния екран на Customize. Маркираната област е филтрирана.
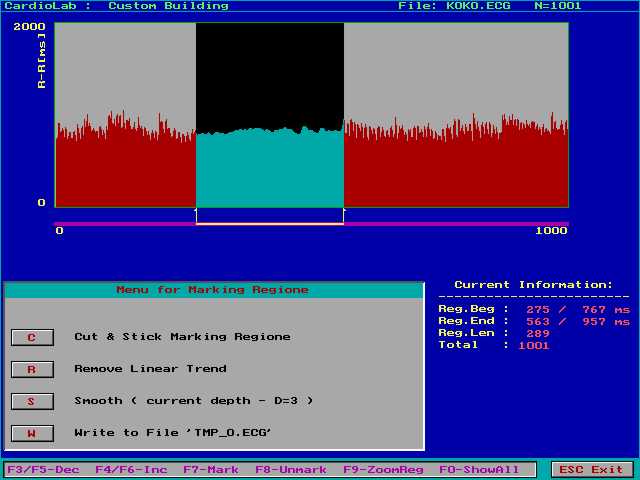
фиг.3.1
Изброените до тук операции могат да се приложат само върху маркиран регион (F7 - маркира избрания регион). Ако искаме да променим ръчно някой R-R интервал просто местим стрелката под него и чрез клавишите горна и долна стрелка (или Ins и Del за по-груба стъпка) го променяме.
Функцията дава възможност и за така наречената 'лупа' т.е. увеличаване на даден участък в целия прозорец. За целта не е необходимо да се маркира избрания участък, а само се натиска F9. Дълбочината на влагане на операцията 'лупа' е неограничена т.е. след като е увеличен даден участък отново може да се избере по-малък регион от него, който да се разшири и т.н. При излизане от 'Customize' се чака потвърждение за актуализиране на данните в паметта. Ако отговора е положителен данните се променят съобразно с направените изменения и всички останали режими вече работят с тези данни. При отрицателен отговор (или произволен клавиш) промените, които са направени в режима 'Customize' се игнорират и данните остават непроменени.
2.2.2. Trend Separation - отделяне на тренд.
След изпълнение на тази функция, данните в паметта се преработват като им се премахва линейния тренд.
Тази функция се различава от функцията, предвидена в режим 'Customize' за изчистване на линейния тренд, която работи с линейна регресия.
Премахването на линейния тренд при този режим, се извършва чрез диференциране (диференчното уравнение бе дадено по-рано в обзора на методите за обработка на сигнали).
2.2.3. Artefacts Clean - премахване на артефакти.
Премахва артефактите и дава отчет за техния брой, а така също и средната дължина на R-R интервалите и средно-квадратичното отклонение
2.3. STATISTICS - изчислява статистически параметри.
2.3.1. Normal Statistics - изчислява стандартни статистически показатели:
Number of R-R
intervals.......: 159
Mean heart rate [b/min] ......: 97.778
Mean R-R Interval length [ms] : 613.635
Standart Deviation ...........: 20.528
Variance (StD/MeanRR) ........: 3.34531 %
Skewness .....................: 0.396876
Kurtosis .....................: 0.415076
Min R-R Interval length [ms] .: 568
Max R-R Interval length [ms] .: 678
Range (MaxRR-MinRR) [ms] .....: 110
Това са - брой R-R интервали, средна честота на сърдечния ритъм (в удари/мин.), средна дължина на R-R интервалите, средноквадратично отклонение, относителна вариация, асиметрия, ексцес, минимална и максимална стойност на R-R интервалите, и размах.
2.3.2. Short & Long Term Variability - изчислява някои специфични (за анализ на R-R интервали) статистически показатели, които дават по-пълна представа за характеристиките на процеса.
Number of R-R
intervals .................: 145
Mean heart rate [b/min] .................: 64.7616
Mean heart rate variability .............: 0.531034
Standart deviation of diferences ........: 664.766
Root mean squaere of diferences .........: 55.3997
Coefficient of variation of diferences ..: 5.94449
Differential index ......................: 29.9513
Vector angle index ......................: -0.02066
Root mean squaere of diff. from the mean : 70.4853
Heart rate standart deviation ...........: 61.1901
Corometric of instantaneous heart rate ..: 153.453
Vector length index .....................: 1697.4
1.Spectral Analysis
2.Linear Trend Detect
3.Extrasystoles Detect (R)
4.Distribution Test (R)
2.4.1. Spectral Analysis - спектрален анализ. Този режим дава възможност да се направи спектрален анализ на произволно избрана област от данните, които се намират в паметта на компютъра. Спектъра може да се получи като амплитуден спектър (AD) или като спектрална плътност (PSD). Може да се получат отношенията на мощностите на две произволно избрани честотни области, а така също и каква част от целия спектър са тези области в проценти.
Съществуват 4 предварителни обработки на данните, които могат да се разрешават или забраняват чрез опции. Тези обработки се извършват непосредствено преди да се изчисли спектъра и не се отразяват на данните в паметта.
Първата обработка е 'допълване с нули'. Тя се извършва винаги когато броят на данните, които са избрани, не е степен на 2 и този брой се прави равен на най-близкото (по-голямо) число, което е точна степен на 2. Чрез опцията 'Z' може изкуствено да се увеличи многократно броя на изчисляваните данни (макс. до 1024). По този начин се увеличава разделителната способност на спектъра (в честотната област отчетите се намират по нагъсто).
Втората обработка е 'подтискане на реда'. Както вече беше споменато това се прави с цел да се предотврати 'изтичането на мощност' в спектъра. Опцията, с която се разрешава тази обработка е 'Т' (по подразбиране тя е разрешена).
Третата обработка е 'премахване на линейния тренд'. Тя е необходима защото предварителното премахване на тренда от всички данни не може да се пребори с локалния тренд, който съществува в отделни къси участъци. Опцията за тази обработка е 'R' (по подразбиране е забранена).
Четвъртата обработка е 'изглаждане'. Тя се извършва върху изчислените стойности на спектралната плътност и нейната дълбочина може да се променя чрез опцията 'S' (по подразбиране тя е 3 и може да се променя максимум до 9).
Честотния диапазон, в който се получава спектъра може да се променя чрез такта на дискретизация (Td), чрез който се извършва трансформирането на данните във времеви ред. За начина на промяна на Td ще стане дума по-надолу.
Предвидена е възможност за наслагване на графиките (като е възможно да се промени и линията, с която се изчертава всяка една от тях). Това дава възможност да се сравнят спектрите на различни участъци от данните.
2.4.2. Linear Trend Detect - изчислява параметрите на линейния тренд без да го премахва. Използва се линейна регресия.
1.Scatter Plot
2.Ritmogram
3.Hystogram
4.All Graphics
5.Scatter_3D
В този режим потребителя има възможност за графично представяне на данните във вид на скатерограма, ритмограма, хистограма и обемна скатерограма.
2.5.1. Scatter Plot - тази функция показва две скатерограми. Едната е скалирана относително спрямо минимума и максимума на данните, което позволява да се се направи по-пълен анализ на образа, който е получен. Другата графика е скалирана абсолютно (за минимум е взета нулата а за максимум 2000), и е удобна за сравнение на скатерограми от различни записи.
2.5.2. Ritmogram - отново имаме две графики с различно скалиране поради съображенията, посочени по-горе. Предвижда се в бъдещото разширение на системата тук да се включат допълнителни обработки на полученото изображение, които да дадат по-подробна информация за характера на данните.
2.5.3. Hystogram - и тази функция не прави изключение от горните две по отношение на скалирането. Тук се дава допълнителна информация за модата и нейната амплитуда, а така също и широчината на интервалите, на които е разделена хоризонталната ос (дължината на R-R интервалите в ms).
2.5.4. All Graphics - Показва всички изброени по-горе графики плюс графиката на спектралната плътност (при такт на дискретизация равен на средната дължина на R-R интервалите) на един екран.
За да могат да се сравняват различните графики от едни и същи данни, а освен това и графиките, получени от различни записи отново се използва едновременно абсолютно и относително скалиране (изключение прави графиката на спектралната плътност, която е дадена само в относително скалиране т.к. при нея е по-важно да се види честотата на отделните пикове, отколкото тяхната абсолютна амплитуда).
Тук се дават и някои допълнителни показатели - минималната, максималната и средната дължина на R-R интервалите (в msec и удари/мин.). Показана е и продължителността на изследвания период в минути.
2.5.5. Scatter_3D - Изобразява скатерограмата в тримерното пространство (получава се всъщност тримерна хистограма), като с това дава възможност да се получи по-ясна представа за разположението и 'мощността' на отделните области (ако има такива) от двумерната скатерограма. Дава се стойността на модата (най-високия стълб) и широчината на интервалите, на които е разделена областта между минималния и максималния R-R интервал.
2.5.6. Spectrum_3D - Този режим беше добавен по-късно. Изобразява спектрограмата в тримерното пространство.
1.Time Discret.
2.Sound Off/On
3.Printer Off/On (R)
4.Spectrum (R)
2.6.1. Time Discret. - интервал на дискретизация. Дава възможност да се променя Td (от 50 до 5000 мсек. или в честота от 0.2 до 20 Hz). Това позволява да си изберем интересуващия ни честотен диапазон.
Например ако ни интересуват само бавните вълни в сърдечния ритъм, бихме могли да изберем по-голям такт на дискретизация, при който целия честотен диапазон ще обхваща само областта на бавните вълни. По този начин може да се направи разграничение на бавните вълни от различен порядък, които при един по-широк честотен диапазон биха изглеждали като един единствен пик.
2.6.2. Sound Off/On - забранява/разрешава звуковия сигнал.
1.Window's Color
2.Window's Frame
3.Timer Const.
4.Data Port
5.Save config
6.Load config
2.7.1. Window's Color - дава възможност да се променят цветовете на прозорците. Това е особено полезна функция когато се работи с черно-бял монитор.
2.7.2. Window's Frame - дава възможност да се променят рамките на прозорците. По този начин се преодолява неудобството при работа с различни кодови таблици.
2.7.3. Timer Const. - променя константата, която инициализира таймера. По подразбиране стойността на Timer_con=1193 (тази стойност инициализира таймера така, че той да издава прекъсване на всяка 1 мсек.). Тази функция позволява да се направи точна калибровка, ако се разполага с прецизен източник на временни интервали.
2.7.4. Data Port - избор на паралелен порт, от който ще се четат данните.
2.7.5. Save config - записва описаните по-горе параметри в конфигурационен файл.
2.7.6. Load config - прочита конфигурационен файл от диска и преконфигурира системата спрямо него.
1.From ECG
2.From EEG (R)
3.Simulation
2.8.1. From ECG - чете данни от ЕКГ-монитор (или идентификатор на R-R интервали). Задава се името на файла и броя на R-R интервалите, които ще се запишат.
По време на записа не трябва да се натискат никакви клавиши, освен ако е необходимо записът да бъде прекъснат (при прекъсване на записа данните не се губят).
При появяване на недопустимо дълъг R-R интервал се шчита, че има повреда в хардуера и записа автоматично се прекратява като се издава съответното съобщение.
2.8.2. From EEG (R) - запазен режим за бъдещи разширения на системата (за четене на данни от ЕЕГ монитор).
2.8.3. Simulation - симулира данни (сбор от две синусоиди и бял шум) за тестване на системата.
F(i)=Ao+A*sin(2*PI*f1*i)+A*sin(2*PI*f2*i)+RND(n)
Във всички, описани по-горе режими, се прави анализ на въвежданите от потребителя данни и параметри за управление на системата. При некоректна работа се издават съответни съобщения за грешка, а там където е възможно се извършва автоматична корекция.
За проверка работоспособността на системата бяха извършени редица експерименти с данни, симулирани от компютъра (виж Глава 3 режим Simolation). Усилията бяха насочени главно към спектралния анализ, който (както вече беше споменато в предните глави) е най-мощния, но в същото време и най-капризния метод.
Основна цел при използването на спектралния анализ е да се открият хармоничните съставки в сигнала. На фиг.4.1 е показан амплитудния спектър (квадратен корен от спектралната плътност на мощността, по-надолу за краткост ще употребявам само спектър) на входен сигнал, образуван като сума от две синусоиди с честоти съответно f1=0.2 Hz и f2=0.4 Hz.
фиг.4.1
Под графиката на спектъра за по-голяма яснота се дава и изходния ред под формата на относителнно скалирана ритмограма.
Спектралната плътност на същия сигнал, само че зашумен (с адитивен шум с равномерно разпределение) е показана на фиг.4.2
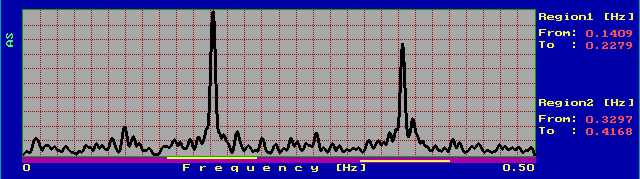
фиг.4.2
Доминиращи са отново пиковете на двете основни съставки.
След пропускане на горния сигнал (от фиг.4.2) през нискочестотен филтър (чрез режим Customize), от неговия спектър изчезва пикът, съответстващ на честота 0.4 Hz.
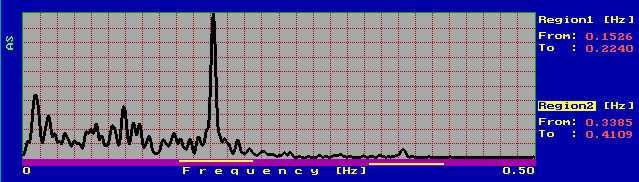
фиг.4.3
Понякога се налага промяната на честотния диапазон на спектъра с цел разграничаване на два (или повече) пика, разположени близко един до друг. На фиг.4.4 е показан спектъра на тестващ сигнал, с честоти на съставящите го хармоници f1=0.01 Hz и f2=0.02 Hz, при Td=1000 msec.
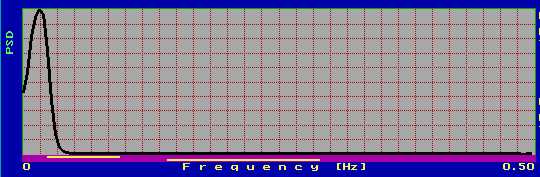
фиг.4.4
Както се вижда, двата пика са твърде близо и не са ясно разграничени (в някои случаи те дори няма и да личат). Следователно за да се видят по-добре е необходимо да 'разтегнем' честотната скала. Това става чрез увеличаване на такта на дискретизация. На фиг.4.5 е показан спектъра при Td=10000.
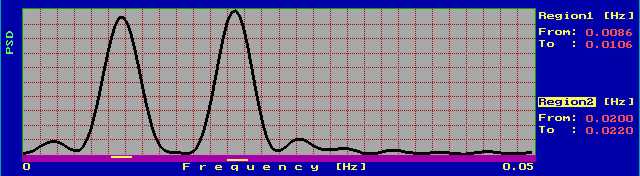
фиг.4.5
Следващата графика (фиг.4.6) илюстрира ефекта от премахването на линейния тренд (опция R). За тестов сигнал се използва сума от две синусоиди с честоти f1=0.001 Hz и f2=0.1 Hz (амплитудата на f1 е многократно по-голяма от тази на f2). Избран е такъв участък от данните (бялата лента под тях), който да симулира силен линеен тренд.
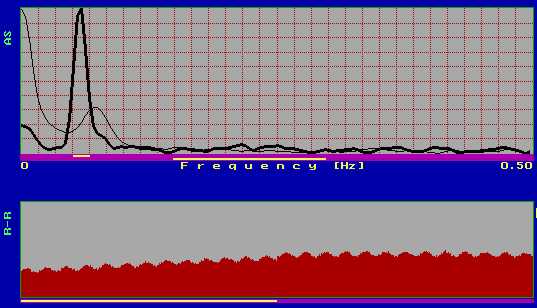
фиг.4.6
По-тънката линия представя спектъра преди премахването на линейния тренд. Вижда се, че пикът съответстващ на честота 0.1 Hz е силно подтиснат. След премахване на лин. тренд (по-дебелата линия) този пик силно се откроява.
В тази точка ще опиша два, различни по своя характер експеримента, реализирани с помоща на системата CardioLab. Целта е да се демонстрират възможностите на системата да се справя с подобни задачи
Този експеримент е извършен от д-р Л.Грънчаров (научен център на ЦСКА), по стандартна методика: на изследваното лице се прилага стъпаловидно велоергометрично натоварване до отказ. Началното натоварване е 60 вата като на всеки 90 сек. се увеличава с 30 вата.
фиг.4.7
На фиг.4.7 е показана ритмограмата, на която могат да се видят преходните процеси при промяна на натоварването. Най-ясно се вижда преходният процес на първото стъпало (близо до началото), който е силно колебателен. На фиг.4.8 и фиг.4.9 са показани хистограмата и обемната скатерограма на данните.
фиг.4.8
фиг.4.9
За да проследим промяната в регулационните функции на организма при натоварване ще направим спектрален анализ на реда от R-R интервали (ще вземем отрязък за по-лесно). От ритмограмата се вижда, че линейния тренд е твърде силен и затова опцията R (за премахване на линеен тренд) трябва да е включена. Резултатите от спектралния анализ са показани на фиг.4.10.
фиг.4.10
С плътната тънка линия е представен спектъра на най-ниското стъпало (от трите изследвани), с пунктираната линия- следващото след него и с плътната широка линия е спектърът на последното стъпало, което е с няколко нива по-високо от второто.
От графиката се вижда, че с увеличаване на натоварването дихателните вълни се изместват надясно по честотната ос, а бавните вълни - наляво. От тук могат да се свалят няколко параметъра, които характеризират регулаторните функции на изследвания спортист. Например скорост на изместване на дихателните (респективно бавните) вълни, промяна в мощностните съотношения между различните вълни и т.н.
При практикуване на ТМ [35] се достига до състояние 'restful alertness' [36], което е различно от всички познати до момента състояния (сън, бодърствуване и т.н.). Този феномен се изучава задълбочено от редица институти, между които най-реномираният е Maharishi International University (Fairfield, Iowa - USA) със своите филиали в Холандия, Швейцария, Германия, Англия и т.н. Резултатите от проведените изследвания се публикуват в специализирани издания на университета [36,37].
Изследванията, които са проведени (д-р Е.Павлова, д-р Л.Петров и д-р Л.Грънчаров) с помощта на системата CardioLab върху 15 души, практикуващи ТМ, имат за цел да дадат представа за динамиката в регулацията на сърдечния ритъм по време на медитация.
На фиг.4.11 е показан спектърът на данните, записани преди медитация, фиг.4.12 - по време на медитация и фиг.4.13 - след медитация. На всички графики има по два спектъра, съответстващи на началото (по-тънката линия) и края (по-дебелата линия) на съответния запис. Това е направено с цел да се обхванат по-пълно трите цикъла (преди, по време и след) от цялостния процес на медитация. И тъй-като началото на всеки цикъл е повлияно от предходния такъв, то за характера на съответния цикъл трябва да съдим по неговия край (където остатъчното влияние е най-слабо).
фиг.4.11
фиг.4.12
фиг.4.13
От графиките се вижда, че бавните вълни по време на медитация, увеличават своята мощност. След медитацията дихателните вълни отново преобладават.
Правени са регистрации на дишането по време на ТМ [34], които показват подобна редукция на амплитудата и честотата. Интерес представлява по-нататъшното изследване и интерпретация на бавно-вълновите компоненти в спектъра, което излиза извън рамките на настоящия труд.
1. DeBoer R, Karemaker J, Strackee J, Comparing spectra of series of point events particulary for heart rate variability data. IEEE Trans. Biomedical Engineering, Vol.31, No.4, April 1984.
2. Nollo G, Speranza G, Grasso R, Bonamini R, Mangiardi L, Antolini R, Spontaneous beat-to-beat variability of the ventricular repolarization duration. Journal of Electrocardiology Vol.25 No.1 January 1992.
3. Rompelman O, Hordijk W, New method for the assessment of neonantal respiratory sinus arrhythmia. Trans. Med. & Biol. Eng. & Comput. September 1987, 25.
4. Pagani M, Lombardy F, Guzzetti S et al, Power spectral analysis of heart rate and arterial pressure variabilities as a maker of sympato-vagal interactions in man and conscious dog. Circulation Res. Vol.59, No.2 August 1986.
5. Wei L, Chow P, Frequency distribution of human pulse spectra. IEEE Trans. Biom. Eng. Vol.32, No.3, March 1985.
6. Anan T, Nakagaki O, Nakamura M, An application of lorenz and multi-lorenz plot to computerized analysis of arrhythmia. Japanese Heart Journal Vol.23, 1982
7. Rompelman O, Snijders J, Spronsen C, The measurment of heart rate variability spectra with the help of a personal computer. IEEE Trans. Biom. Eng., Vol.29, No.7, July 1982.
8. Inoue K, Miyake S, Kumashiro M, Ogata H, Yoshimura O, Power Spectral Analysis of Heart Rate Variability in Traumatic Quadriplegic Humans. Copyright (c) 1990 the American Physiological Society.
9. Воскресенский А, Вентцел М, Статистический анализ сердечного ритма и показателей гемодинамики в физиологических исследованиях/Проблемы космической биологии. Том.26, Москва "Наука", 1974.
10. Кутерман Э, Хаспекова Н, Закономерности взаимосвязанных изменений амплитуды и частоты колебательных составляющих ритма сердца. Физиология человека Том.15, Но.5, 1989.
11. Кутерман Э, Носов М, Исследование математической модели синусого ритма сердца. Кардиология Том.25, Но.5, 1984.
12. Нидеккер И, Шукаров Ф, ЭВМ-методика нахождения амплитудно-частотных характеристик кардиореспираторной системы в задаче адаптации к высокогорью. УДК 612.172.2 : 518.5 : 519.25, Москва 1987.
13. Казин Э, Рифтин А, Федоров А, Панферов В, Шорин Ю, Автоматизированиые системы в комплексной оценке здоровья и адаптивных возможностей человека. Физиология человека, Том.16, Но.3, 1990.
14. Коркушко О, Шатило В, Особенности переходново процесса сердечного ритма при активной ортостатической пробе у людей пожилого и старческого возраста. Физиология человека, Том.15, Но.4, 1989.
15. Рифтин А, Модел разпознавания функциональных состояний организма на основе математического анализа сердечного ритма., Физиология человека, Том.16, Но.3, 1990.
16. Лосев В, Микропроцессорные устройства обработки информации. Алгоритмы цифровой обработки., Минск "Вышэйшая школа", 1990.
17. Bracewell R, The Hartley transform., Oxford University Press. New York 1986. превод на руски А.Папкова, Преобразование Хартли - теория и приложения., Москва "Мир" 1990.
18. Претт У, Цифровая обработка изображении., Москва "Мир"-1982.
19. Конов К, Голденберг Л, Устройства за цифрова обработка на сигнали., ДИ Техника, София 1988.
20. Калайков И, Ищев К, Гарипов Е, Андреев Х, Сборник алгоритми и програми по проектиране на системи за автоматично управление. Цифрова обработка на сигнали. ДИ Техника, София 1988.
21. Томов И, Марков С, Александрова З, Александров А, Микро-процесорни управляващи системи., ДИ Техника, София 1986.
22. Въндев Д, Матеев П, Статистика с "Правец-82", Наука и изкуство, София 1988
23. Pinciroli F, Graphic techniques and derived sequences for the observation of R-R interval values., Elsevier Science Publishers B.V.(North Holland) IFIP-IMIA,1984.
24. Рифтин А, Выявление характера экстрасистолии по резултатам выполнения функциональных проб., Физиология человека, Том.17, Но.4, 1991.
25. Douglas A at al, An approach to cardiac arrithmia analusis using hidden Markov models., Biom. Eng. Vol.37, No.9, September 1990.
26. Cahill S, Mithel R, Sharif B, Jenkins J, Acquisition and analysis of heart rate variability signals., Automedica, Vol.13, No.2,3, 1991.
27. Венков , Избрани глави от математиката., Лекционен курс ТУ-София 1988.
28. Калайков И, Сигнали и системи., Лекционен курс ТУ-София 1988.
29. Калайков И, Методи за обработка на експериментални данни., Лекционен курс ТУ-София 1989.
30. Berger R, Saul J, Cohen R, Transfer function analysis of automatic regulation. Canine atrial rate response., Copyright (c) 1989 the American Physiological Society
31. Saul J, Berger R, Chen M, Cohen R, Transfer function analysis of automatic regulation. Respiratory sinus arrhythmia., Copyright (c) 1989 the American Physiological Society
32. Томов И, Електрокардиология., Медицина и фискултура, София 1980.
33. Hyndman B, Mhon R, A pulse modulator model of pacemaker aktivity., in Dig. 10th Int. Conf. Med. Biol. Eng., Dresden, Germany,, 1973
34. Farrow J, Hebert J, Breath suspension during the Transcendental Meditation technique., Psihosomatic Medicine 44, 1982.
35. Maharishi Mahesh Yogi, Science of being and fit of living. Transcendental Meditation., New York, 1968.
36. Scientific research on the Maharishi technology of the unified field : The Transcendental Meditation and TM-Sidhi program., Maharishi's second year of world peace, 1988.
37. Modern science and vedic science., Maharishi International University, Faifield, Iowa, USA.
Можете да изтеглите програмата от адрес: http://mlab.my.contact.bg/dwork/clab.zip
Последната модификация на
този документ е правена на 5 Юни 2004 г.
mlab-AT-mail-DOT-bg